Suppose that there is a series of “n” payments uniformly spaced but differing from one period to the next by a constant. The change or “gradient” from one period to the next is denoted “G.” Let A1 be the payment at EOY 1.

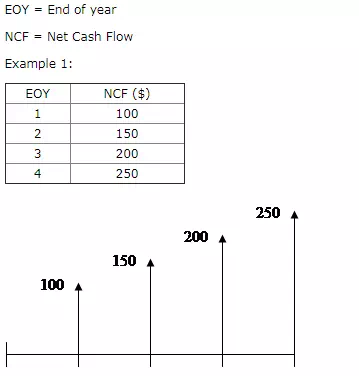
A1 = $100; G = + $50; i = 7%

P = A1 (P/A,i%,n) + G (P/G,i%,n)

Note that you must subtract the annual amount, A1, from all annual amounts before applying the gradient factor.

P = 100 (P/A,7%, 4) + 50 (P/G, 7%, 4)

P = 100 (3.387) + 50 (4.795)

P = 578.45

Geometric Gradient Series

Suppose that there is a series of “n” payments uniformly spaced, but differing from one period to the next by a constant multiple. The change or “gradient” multiple from one period to the next is denoted “g.” There will, of course, also be an interest rate “i” that applies.

g = gradient percent (as a decimal in calculations)

i = interest percent (as a decimal in calculations)

n =number of periods

A1 = payment at EOY 1

The Present Worth (P) is given by:

P = A1 ( P/ A1, g, i, n ) = A1 [ 1 – ( 1 + g ) n ( 1 + i ) –n ] / ( i – g )

Example 1: A1 = $100; g = 15%; i = 9%; n = 5

P = A1 ( P/ A1, g, i, n ) = 100 [ 1 – ( 1 + 0.15 ) 5 ( 1 + 0.09 ) –5 ] / ( 0.09 – 0.15 )

= 100 [ 1 – 2.0114 * 0.6499] / (-0.06)

= 100 [-0.3072] / (-0.06)

= 512.1

Example 2: A1 = $100; g = 5%; i = 8%; n = 10

P = A1 ( P/ A1, g, i, n ) = 100 [ 1 – ( 1 + 0.05 ) 5 ( 1 + 0.08 ) –5 ] / ( 0.08 – 0.05 )

= 100 [ 1 – 1.628894627 * 0.463193488] / (0.03)

= 100 [ 0.2455] / (0.03)

= 818.3554