In this type of investment mode, the objective is to find the equivalent amount (A) that should be deposited at the end of every interest period for n interest periods to realize a future sum (F) at the end of the nth interest period at an interest rate of i.

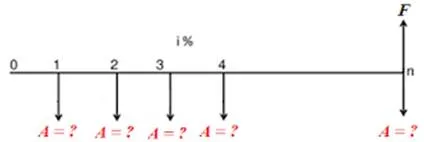
Cash flow diagram of equal-payment series sinking fund

Here,

     A = equal amount to be deposited at the end of each interest period

         n = No. of interest periods

         i = rate of interest

         F = single future amount at the end of the nth period

The formula to get F is

A = (F * i) /   [(1 + i)n – 1] =F (A/F, i, n)

Where

(A/F, i, n) is called as equal-payment series sinking fund factor.

Example problem on equal-payment series sinking fund

A company has to replace a present facility after 12 years at an outlay of Rs. 4,00,000. It plans to deposit an equal amount at the end of every year for the next 12 years at an interest rate of 16% compounded annually. Find the equivalent amount that must be deposited at the end of every year for the next 12 years.

Given data

n = 12 years

F = Rs. 4,00,000

i = 16%

To find

A

Formula used

A = F (A/F, i, n)

Solution

A         = F (A/F, i, n)

                        = 4,00,000 (A/F, 16%, 12)

                        = 4,00,000 * 0.0324

           A         = Rs. 12,960

Result

            The company should deposit an equal amount Rs. 12,960 at the end of every year for the next 12 years at an interest rate of 16% to get an outlay Rs. 4,00,000.