In finance, the equivalent annual cost (EAC) is the cost per year of owning and operating an asset over its entire lifespan. It is calculated by dividing the NPV of a project by the “present value of annuity factor”:

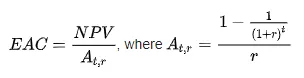
where r is the annual interest rate and

t is the number of years.

Alternatively, EAC can be obtained by multiplying the NPV of the project by the “loan repayment factor”.

EAC is often used as a decision making tool in capital budgeting when comparing investment projects of unequal lifespans. However, the projects being compared must have equal risk: otherwise, EAC must not be used.

The technique was first discussed in 1923 in engineering literature, and, as a consequence, EAC appears to be a favoured technique employed by engineers, while accountants tend to prefer net present value (NPV) analysis.Such preference has been described as being a matter of professional education, as opposed to an assessment of the actual merits of either method.In the latter group, however, the Society of Management Accountants of Canada endorses EAC, having discussed it as early as 1959 in a published monograph

v Application

v  EAC can be used in the following scenarios:

v  Assessing alternative projects of unequal lives (where only the costs are relevant) in order to address any built-in bias favouring the longer-term investment.

v  Determining the optimum economic life of an asset, through charting the change in EAC that may occur due to the fluctuation of operating costs and salvage values over time.

v  Assessing whether leasing an asset would be more economical than purchasing it.

v  Assessing whether increased maintenance costs will economically change the useful life of an asset.

v  Calculating how much should be invested in an asset in order to achieve a desired result (i.e., purchasing a storage tank with a 20-year life, as opposed to one with a 5-year life, in order to achieve a similar EAC).

v  Comparing to estimated annual cost savings, in order to determine whether it makes economic sense to invest.

v  Estimating the cost savings required to justify the purchase of new equipment.

v  Determining the cost of continuing with existing equipment.

v  Where an asset undergoes a major overhaul, and the cost is not fully reflected in salvage values, to calculate the optimum life (i.e., lowest EAC) of holding on to the asset.

A practical example

A manager must decide on which machine to purchase, assuming an annual interest rate of 5%:

Option	Machine A	Machine B
Investment cost	$50,000	$150,000
Expected lifetime	3 years	8 years
Annual maintenance cost	$13,000	$7,500
Equivalent annual cost	{\displaystyle {\frac {\$50\,000}{A_{3,5}}}+\$13\,000=\$31\,360}	{\displaystyle {\frac {\$150\,000}{A_{8,5}}}+\$7\,500=\$30\,708}

The conclusion is to invest in machine B since it has a lower EAC.