In order to evaluate investment alternatives, sums of money produced at different points in time must be compared. This is only possible if their characteristics are analysed on an equivalent basis. Two situations are equivalent when they have the same effect, the same worth or the same value. Three factors are involved in the equivalence of investment alternatives:

Ø  the amount of money

Ø  the time of occurrence

Ø  the rate of interest

The factors of interest which will be developed take account of duration and rate of interest. Later, they are used in the transformation of alternatives in terms of a common time-base.

Derivation of Interest Factors

      Interest factors applicable to routine situations, such as compound interest with single payment, and with a series of equal payments, will be derived. The following five points must be kept in mind for application in calculations of investment alternatives:

      The end of one period is, at the same time, the beginning of the next period.

      P is produced at the beginning of a period, at a time in the present;

      F occurs at the end of the nth period, from a time considered as present (n being the total number of periods).

      A is a single payment within a series of equal payments made at the end of each period under consideration. When P and A occur together, the first A in the series is produced one period after P. When F and A occur together, the last A in the series occurs at the same time as F. If the equal payments series occurs at the beginning of each period under consideration, it is called Ab.

      In proposing different alternatives, the quantities P, F, A and Ab must be used such that they incorporate the conditions needed to adjust the respective models to the factors used.

Table B.2 summarizes the financial equations that show the relationships between P, F and A (Jelen and Black, 1983).

Table B.2 Financial Equations

Single -payment compound-amount factor:
Given P, find F	F = P ×  [(1+ i)n]	F = P × FPF,i,n
Single -payment present-worth factor:
Given F, find P	P = F × [(1+ i)n]	P = F × FFP,i,n
Equal-payment series  present-worth factor:
Given  A, find P		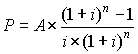P = A × FAP,i,n
Equal-payment series  capital-recovery factor:
Given  P, find A		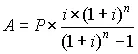A = P × FPA,i,n
Equal-payment series-compound-amount factor:
Given  A, find F		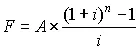F = A × FAF,i,n F = A × FAP,i,n ×  FFP, i, n
Equal-payment series  sinking-fund factor:
Given F, find A		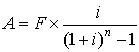A = F × FFA, i, n A = F × FFP, i, n × FPA, i, n